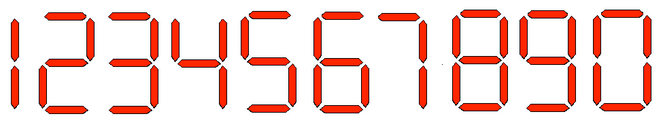Funções¶
Função é uma sequência de instruções que executa uma operação de computação. Ao definir uma função, você especifica o nome e a sequência de instruções. Depois, pode utilizar (“chamar”) a função pelo nome.
A ideia é similar às funções matemáticas! Mas funções em uma linguagem de programação não realizam necessariamente apenas cálculos.
Vimos o type(), um exemplo de função:
>>> type(23)
<class 'int'>
>>> type('textinho')
<class 'str'>
Definindo funções¶
Se quisermos uma função que ainda não existe em Python, temos que definí-la.
Criando uma função simples:
def NOME_DA_FUNÇÃO(LISTA DE PARÂMETROS):
COMANDOS
Aviso
Coloque os dois pontos após definir a função!
Nota
Faça a indentação nas linhas abaixo da definição da função!
>>> def soma():
... print(1 + 1)
...
>>> soma()
2
>>> def soma():
... return 1 + 1
...
>>> soma()
2
Qual a diferença entre utilizar print() e return() aqui em cima?!?
>>> def imprime_letra():
... print("If you didn't care what happened to me. And I didn't care for you")
...
>>> imprime_letra()
If you didn't care what happened to me. And I didn't care for you
>>> type(imprime_letra)
<class 'function'>
>>> def repete_letra():
... imprime_letra()
... imprime_letra()
...
>>> repete_letra()
If you didn't care what happened to me. And I didn't care for you
If you didn't care what happened to me. And I didn't care for you
Funções com argumentos¶
Queremos somar 3 com um número qualquer que insiro na função. Bora lá:
>>> def soma_valor(x):
... return 3 + x
...
>>> soma_valor(5)
8
>>> z = soma_valor(10)
>>> z
13
Que sem graça! Quero somar dois números quaisquer!
>>> def soma_dois_numeros(x, y):
... return x + y
...
>>> soma_dois_numeros(7, 4)
11
Tenho dificuldade com a tabuada do 7! Ajude-me!
>>> def tabuada_do_7():
... for i in range(11):
... print (7 * i)
...
>>> tabuada_do_7()
0
7
14
21
28
35
42
49
56
63
70
Mai tá legal isso! Quero a tabuada do 1 ao 10 agora! Bora!
>>> def tabuadas():
... for i in range(1, 11):
... for j in range(1, 11):
... print("{} * {} = {}".format(i, j, i * j))
...
>>> tabuadas()
1 * 1 = 1
1 * 2 = 2
1 * 3 = 3
1 * 4 = 4
1 * 5 = 5
1 * 6 = 6
1 * 7 = 7
1 * 8 = 8
1 * 9 = 9
1 * 10 = 10
2 * 1 = 2
2 * 2 = 4
2 * 3 = 6
2 * 4 = 8
2 * 5 = 10
2 * 6 = 12
2 * 7 = 14
2 * 8 = 16
2 * 9 = 18
2 * 10 = 20
3 * 1 = 3
3 * 2 = 6
3 * 3 = 9
3 * 4 = 12
3 * 5 = 15
3 * 6 = 18
3 * 7 = 21
3 * 8 = 24
3 * 9 = 27
3 * 10 = 30
4 * 1 = 4
4 * 2 = 8
4 * 3 = 12
4 * 4 = 16
4 * 5 = 20
4 * 6 = 24
4 * 7 = 28
4 * 8 = 32
4 * 9 = 36
4 * 10 = 40
5 * 1 = 5
5 * 2 = 10
5 * 3 = 15
5 * 4 = 20
5 * 5 = 25
5 * 6 = 30
5 * 7 = 35
5 * 8 = 40
5 * 9 = 45
5 * 10 = 50
6 * 1 = 6
6 * 2 = 12
6 * 3 = 18
6 * 4 = 24
6 * 5 = 30
6 * 6 = 36
6 * 7 = 42
6 * 8 = 48
6 * 9 = 54
6 * 10 = 60
7 * 1 = 7
7 * 2 = 14
7 * 3 = 21
7 * 4 = 28
7 * 5 = 35
7 * 6 = 42
7 * 7 = 49
7 * 8 = 56
7 * 9 = 63
7 * 10 = 70
8 * 1 = 8
8 * 2 = 16
8 * 3 = 24
8 * 4 = 32
8 * 5 = 40
8 * 6 = 48
8 * 7 = 56
8 * 8 = 64
8 * 9 = 72
8 * 10 = 80
9 * 1 = 9
9 * 2 = 18
9 * 3 = 27
9 * 4 = 36
9 * 5 = 45
9 * 6 = 54
9 * 7 = 63
9 * 8 = 72
9 * 9 = 81
9 * 10 = 90
10 * 1 = 10
10 * 2 = 20
10 * 3 = 30
10 * 4 = 40
10 * 5 = 50
10 * 6 = 60
10 * 7 = 70
10 * 8 = 80
10 * 9 = 90
10 * 10 = 100
Argumento padrão¶
Em alguns casos é conveniente deixar um valor padrão para algum (ou alguns) argumento(s) de uma função. Por exemplo, imagina uma função que soma dois ou três números:
>>> def soma_numeros(x, y, z=0):
... return x + y + z
...
>>> soma_numeros(1, 2, 3)
6
>>> soma_numeros(4, 5)
9
Assim podemos usar a mesma função soma_numeros para somar dois ou três argumentos. Basta definir o valor do argumento na definição da função. Isso só é permitido para os últimos argumentos, ou seja, todos os argumentos à direita de um argumento padrão devem também ser um argumento padrão. Por exemplo:
# argumento 'normal' depois de um padrão
>>> def soma_numeros(x, y=0, z):
... return x + y + z
...
File "<stdin>", line 1
SyntaxError: non-default argument follows default argument
>>> def soma_numeros(x, y=0, z=0):
... return x + y + z
...
>>> soma_numeros(1, 2, 3)
6
É possível também utilizar o retorno de uma função diretamente como argumento de outra. Por exemplo, o resultado da função acima como argumento de uma outra função qualquer. No caso estamos utilizando a mesma função. Assim:
>>> def soma_numeros(x, y):
... return x + y
...
>>> soma_numeros(1, soma_numeros(3, 4))
8
O retorno de soma_numeros(3, 4) é 7. Ao utilizar este valor como argumento da função soma_numeros(1, 7), o retorno é 8.
Recursão¶
Este conceito é uma técnica de programação que envolve «chamar» a mesma função repetidas vezes até chegar na solução.
Nota
Confira sua função recursiva para evitar de cair em um loop infinito!
Para que a função seja aplicada diversas vezes, o retorno da função deve conter a própria função. Por exemplo:
>>> def fatorial(n):
... if n == 1:
... return 1
... else:
... return n * fatorial(n-1)
...
>>> fatorial(3)
6
Vamos entender o que está sendo feito aqui.
O cálculo do fatorial de um número, por exemplo, o fatorial de 3 (ou 3!), é:
3! = 3 * 2 * 1
Por definição:
1! = 1
0! = 1
Então, para obter 3! pela função que escrevemos, o 3 entra como argumento e é analisado no if e «cai» no
else, por não ser igual a 1.
Aqui é que a magia acontece! O retorno desta função será 3 multiplicado pela função fatorial (sendo utilizada
pela segunda vez) que irá fazer o cálculo com 2 agora como argumento. Da mesma forma, cai no else e
multiplica o valor de 2 pelo fatorial(1). Agora esta função «cai» no if e retorna 1. Ao retornar o valor 1 na
função anterior (factorial(2)), é feito o produto de 2 por 1 que resulta em 2. Este valor 2 é utilizado no retorno
da função anterior à esta (factorial(3)), sendo o retorno de 3 por 2, que resulta em 6.
Aqui uma ilustração para compreender estas etapas 1:
Exercícios¶
Faça uma função que determina se um número é par ou ímpar. Use o
%para determinar o resto de uma divisão. Por exemplo:3 % 2 = 1e4 % 2 = 0Faça uma função que calcule a área de um círculo. Insira o raio como argumento.
Dica: faça a importação de
mathe use \(\pi\) de lá.\[A = \pi R^2\]Crie uma função que receba um valor de temperatura em Fahrenheit e transforme em Celsius.
Relembrar é viver:
\[\frac{C}{5} = \frac{F - 32}{9}\]Utilizando a função anterior, faça a impressão da temperatura, em graus Celsius, de 0 °C a 100 °C, e todos os valores correspondentes em Fahrenheit.
Receba uma lista com números inteiros e devolva um número inteiro correspondente à soma dos números recebidos.
Receba uma lista com números inteiros. Verifique se a lista possui números repetidos, caso possua, exclua-os e retorne a lista alterada.
Alanderson quer saber se um endereço IP é válido. Faça um programa para ajudar Alanderson a testar se um endereço é válido.
Para isso, a entrada deve ser um endereço IP (digitado pelo usuário) e o programa deve escrever na tela se é válido ou não. Um endereço IPv4 é composto por 4 números inteiros entre 0 e 255, separados por um ponto.
Por exemplo, o endereço
123.123.123.123é válido, mas666.123.k.3não é.Crie uma função que receba 3 valores e calcula as raízes da fórmula de Bhāskara.
\[x = \frac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a}\]Dica: raiz quadrada é
sqrt(), importandomath:math.sqrt()Faça um teste com
bhaskara(1, -4, -5)e o programa deve obter as raízes: (5.0, -1.0)Escreva uma função que receba um valor de comprimento em centímetros e o transforme em polegadas.
Dica: \(1 pol = 2.54 cm\).
Escreva uma função que receba as dimensões de uma fotografia em centímetros (por exemplo 10 x 15 cm) e a densidade de píxeis da impressora (por exemplo 300 dpi), e retorne a resolução (por exemplo 2.1 mega píxeis) mínima necessária para imprimir aquela foto.
A densidade de píxeis da impressora diz quantos píxeis são impressos a cada polegada. Por exemplo: 300 dpi (dots per inch, ou pontos por polegada) significa que em uma polegada em linha reta da imagem há 300 píxeis.
Dada a função: \(y = 5x + 2\), determine os valores de \(y\) para \(x\) entre -10 a +10, onde \(x\) é inteiro
Escreva uma função chamada
has_duplicatesque tome uma lista e retorneTruese houver algum elemento que apareça mais de uma vez. Ela não deve modificar a lista original.Duas palavras são um “par inverso” se uma for o contrário da outra. Escreva uma função que dado duas palavras, retorne
Truecaso sejam.Escreva uma função que imprime todos os números primos entre 1 e 50
Dica: um número é primo se ele for divisível apenas por 1 e ele mesmo, use o operador
%(resto da divisão) para isso.Duas palavras são anagramas se você puder soletrar uma rearranjando as letras da outra. Escreva uma função chamada
is_anagramque tome duas strings e retorneTruese forem anagramas ouFalsecaso contrário.Escreva uma função que retorne uma lista com todas as chaves de um dicionário que contém um certo valor.
Por exemplo, se o dicionário for
{'a': 1, 'b': 2, 'c': 1, 'd': 4}, a função deve retornar['a', 'c']caso procure pelo valor1;[]caso procure pelo valor666.Escreva uma função que dado um número, calcule o fatorial desse número. Por exemplo, fatorial de 5:
\[5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\]João quer montar um painel de LEDs contendo diversos números. Ele não possui muitos LEDs, e não tem certeza se conseguirá montar o número desejado. Considerando a configuração dos LEDs dos números, faça um algoritmo que ajude João a descobrir a quantidade de LEDs necessário para montar o valor.
Exemplos de entrada e saída:
115380—> 272819311—> 2923456—> 25000—> 18
Crie uma função que aproxima a função matemática seno, utilizando a seguinte equação:
\[\sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\]Essa é a expansão em Série de Taylor da função. Note que esta é uma série infinita! A sua função deve truncar a série em algum momento, ou seja, sua função vai calcular uma aproximação para o seno de um ângulo:
\[\sin(x) \approx \sum_{n=0}^{N} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = \sum_{n=0}^{N} a_n = S_N\]Note que, quanto maior o valor de N, melhor é a aproximação. Mas isso tem um custo: maior vai ser o número de termos nessa série e consequentemente, maior o tempo de execução desse código.
Uma possibilidade é estipular previamente uma precisão a ser atingida pelo código. Ou seja, definimos o desvio máximo \(\epsilon\) que nossa aproximação tem com relação ao valor exato! Isso é feito comparando dois termos consecutivos da série: se a diferença \(\delta\) entre eles (em valor absoluto!) for menor que \(\epsilon\), atingimos a precisão desejada:
\[\delta = | S_N - S_{N-1} |\]Implemente, então, uma função que receba como argumentos:
\(x\): o ângulo (em radianos!!).
\(N_\mathrm{max}\): o número máximo de iterações.
\(\epsilon\): a precisão da aproximação.
e calcule uma aproximação para \(\sin(x)\) usando duas condições de parada: número máximo de termos na série é \(N_\mathrm{max}\) e precisão \(\epsilon\). Ou seja, sua aproximação terá no máximo \(N_\mathrm{max}\) termos, mas pode ter menos termos caso a precisão desejada seja atingida ( \(\delta < \epsilon\)).
Calcule \(\pi\) usando um método de Monte Carlo.
Monte Carlo é uma classe de métodos para resolver problemas usando estatística. Aqui você vai implementar uma função usando um desses algoritmos para calcular o número \(\pi\).
Dado um círculo de raio \(R\) dentro de um quadrado de lados \(2R\), a razão entre a área do círculo para a área do quadrado é:
\[\frac{A_\bigcirc}{A_\square} = \frac{\pi R^2}{4 R^2} = \frac{\pi}{4}\]Ou seja, se você escolher aleatoriamente um ponto dentro do quadrado, a probabilidade dele cair dentro do círculo é de \(\pi / 4\). Se você escolher \(N\) pontos aleatórios dentro do quadrado, cerca de \(N \pi / 4\) estarão dentro do círculo.
Então, basta escolher pontos aleatórios dentro do quadrado e ver se estão dentro do círculo
Um ponto \((x, y)\) está dentro do círculo se \(x^2 + y^2 \leq R^2\).
Faça uma função que receba como argumento um número \(N\) de pontos \((x, y)\) (aleatórios) a serem sorteados. Dentro dessa função, você deve fazer um laço que sorteie esses \(N\) pontos e veja quantos estão dentro do círculo. Se \(M\) pontos caírem dentro do círculo, então a probabilidade de um ponto aleatório estar dentro do círculo é aproximadamente \(M / N\). Então, podemos estimar \(\pi\) como:
\[\pi \approx \frac{4 M}{N}\]Para sortear um número aleatório entre \(a\) e \(b\) utilize a função
uniform(a, b)do módulorandom. Exemplo:>>> import random >>> random.uniform(1, 2) # número aleatório entre 1 e 2 1.8740445361226983
Perceba que ao executar a função
pi()várias vezes seguidas, o resultado é sempre diferente. Então faça um laço para calcularpi()\(K\) vezes, salve os resultados em uma lista e calcule o valor médio e o desvio padrão.Crie uma função que recebe uma palavra. Retorne as letras únicas para a construção desta palavra e a quantidade de cada letra utilizada.
Exemplo de entradas e saídas:
>>> letras_e_quantidades("casa") {'c': 1, 'a': 2, 's': 1} >>> letras_e_quantidades("abracadabra") {'r': 2, 'd': 1, 'a': 5, 'c': 1, 'b': 2}
Tanto cadeias DNA quanto RNA são sequências de nucleotídeos. O DNA é formado por: adenina (A), citosina (C), guanina (G) e timina (T). E o RNA é formado por: adenina (A), citosina (C), guanina (G) e uracila (U).
Dada uma cadeia de DNA, o RNA transcrito é formado substituindo um nucleotídeo pelo seu complemento:
G -> C
C -> G
T -> A
A -> U
Implemente uma função que receba uma cadeia de DNA como string e retorne a o RNA complementar.
Implemente uma função que conte quantas vezes um certo nucleotídeo aparece em uma cadeia de DNA. Para isso, sua função deve receber uma string representando o DNA e outra representando o nucleotídeo. Caso aquele nucleotídeo ou o DNA não seja válido, retorne
None.Nesse exercício, considere como inválido se um nucleotídeo não for
A,C,GouT.O RNA é o responsável por levar as informações contidas no DNA para fora do núcleo da célula, para então ser feita a codificação para as bases púricas: U, A, C e G. Quando arranjadas em sequência de trincas (chamadas códons), formam um polipeptídeo, cadeia de aminoácido. O final de uma cadeia é determinado por um dos seguintes códons:
UGA,UAAouUAG.A tabela a seguir mostra alguns códons e qual aminoácido codifica:
Códon RNA
Aminoácido
UAU
Ile
UGU
Thr
UUG
Asn
UCG
Ser
GUG
His
GCU
Arg
CAU
Val
Por exemplo:
TATTCGCATTGA DNA -> |||||||||||| ATAAGCGTAACT RNA -> UAUUCGCAUUGA Códons RNA -> UAU UCG CAU UGA Polipeptídeo -> Ile-Ser-Val
Faça uma função cuja entrada seja uma string com tamanho múltiplo de 3 que representa o RNA. A saída deverá ser uma string com o nome de cada aminoácido separado por hífen, que representa o polipeptídeo.
Dica: faça um dicionário para trocar os códons por aminoácidos.
Dica2: faça uma lista para facilitar a saída.
Exemplos de entradas e saídas:
>>> polipeptideo("UAUGCUCAUCAUUAUUCGUAG") "Ile-Arg-Val-Val-Ile-Ser" >>> polipeptideo("GCUUAUUCGCAUGCUUCGGCUGCUUAG") "Arg-Ile-Ser-Val-Arg-Ser-Arg-Arg" >>> polipeptideo("CAUUCGGUGGCUUCGGUGUGUCAUUCGCAUUAG") "Val-Ser-His-Arg-Ser-His-Thr-Val-Ser-Val" >>> polipeptideo("GCUCAUUGUUGUUUGCAUUGUGUGGCUGUGCAUUUGUAG") "Arg-Val-Thr-Thr-Asn-Val-Thr-His-Arg-His-Val-Asn"